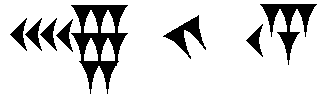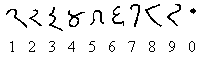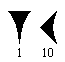Les deux grands types de numération :
|
Numération
additive: |
|
|
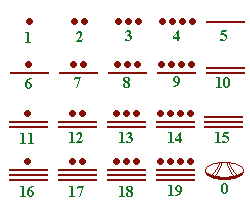
Les chiffres:
|
|
|
On additionne les valeurs de tous les signes utilisés pour écrire le nombre. |
|
|
|
|
|
Q 2 : Écrire
les nombres 10275 et 2000. |
|
|
Numération
de position: Les chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. La valeur
représentée par un chiffre dépend de sa
position. Retenez bien cette méthode qui peut s'appliquer à toute numération de position. |
|
|
Q 6 : Dire simplement, à partir de l'écriture d'un même nombre dans les deux numérations ci-dessus, une raison pour laquelle les numérations de position sont un progrès par rapport aux numérations additives. |
|
|
Numération
romaine:
On remarque l'écriture du chiffre quatre et celle du chiffre neuf. Ce n'est qu'au Moyen-Âge qu'on a écrit les nombres romains tel que IX (neuf), XC (quatre-vingt dix)... Q7 : Expliquer comment est formé le nombre quatre-vingt dix. Donner, avec cette méthode, le nombre 900. Q8
: Cette numération est-elle additive ou de position
?
Q 9 : Écrire
les nombres 1948 et 2001 en numération romaine.
|
Signes
employés: |
|
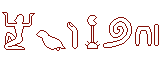
Numération
savante chinoise:
|
|
|
Ainsi,
1987 s'écrit
|
|
|
On
pourrait reprocher à ce système de numération
un risque d'erreur, si l'espace est oublié. L'alternance
des deux types de chiffres évite cette ambiguïté.
Toutefois, le risque existe si deux zéros se suivent,
mais il est impossible de ne pas remarquer le double espace.
ces abaques ont ensuite disparu. |
|
|
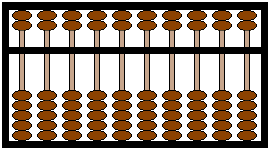
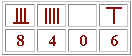
Q 11
: Lire les nombres suivants:
|
|
D'AUTRES EXEMPLES DE NUMERATION :
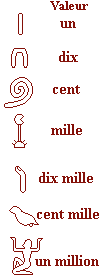
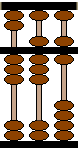
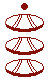
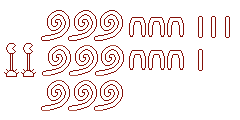 Q1 : Quel est le nombre représenté
ci-contre ?.
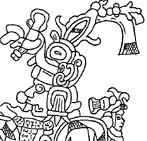
Q1 : Quel est le nombre représenté
ci-contre ?.



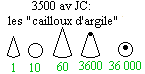
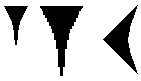
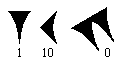
 calame
calame